Linear Regression

Implementing linear regression.

Published

March 15, 2023

Linear Regression

Source code

Implementing linear regression in two ways

1. Analytical formula for \(\hat{w}\)

The first way to implement linear regression is by using the analytical formula that gives us the \(\hat{w}\) to minimize \(L(w)\):

self.w = np.linalg.inv(X_.T@X_)@X_.T@y

2. Gradient descent

We could also use the regular gradient descent to compute \(\hat{w}\). To reduce time complexity, we precompute P = X_.T@X and q = X.T@y, and then pass them to gradient() in the for-loop where we update the gradient:

self.w -= 2*alpha*self.gradient(P, q, self.w)

Experiments

Increasing the number of features

In this experiment, I explore how the training score and validation score change as the number of features increases.

from linear_regression import LinearRegression
from matplotlib import pyplot as plt
import numpy as np

# functions for data generation
def pad(X):
    return np.append(X, np.ones((X.shape[0], 1)), 1)

def LR_data(n_train = 100, n_val = 100, p_features = 1, noise = .1, w = None):
    if w is None: 
        w = np.random.rand(p_features + 1) + .2
    
    X_train = np.random.rand(n_train, p_features)
    y_train = pad(X_train)@w + noise*np.random.randn(n_train)

    X_val = np.random.rand(n_val, p_features)
    y_val = pad(X_val)@w + noise*np.random.randn(n_val)
    
    return X_train, y_train, X_val, y_val

I increase the number of features used in the model from 1 to n_train-1 and plot the change in training and validation scores.

# generate data
n_train = 100
n_val = 100
noise = 0.2
train_scores = []
val_scores = []

# increase p_features from 1 to n_train-1 and calculate training and validation scores for each
for p_features in np.arange(1, n_train): 
    # create data
    X_train, y_train, X_val, y_val = LR_data(n_train, n_val, p_features, noise)
    LR = LinearRegression()
    LR.fit(X_train, y_train)
    train_scores.append(LR.score(X_train, y_train))
    val_scores.append(LR.score(X_val, y_val))


# plot
plt.plot(np.arange(1, n_train), train_scores, label = "Training scores")

# plot
plt.plot(np.arange(1, n_train), val_scores, label = "Validation scores")

xlab = plt.xlabel("Number of features")
ylab = plt.ylabel("Score")
legend = plt.legend()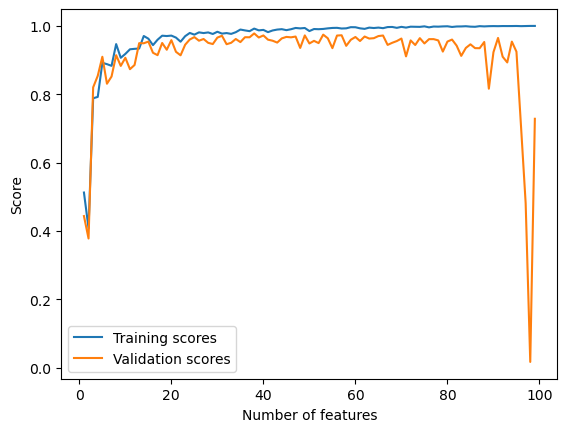

We can observe from the chart that the training score increased all the way to 1.0 as the number of features increases. The validation score, however, has been fluctuating and forms a slightly downward trend, and dramatically decreased to almost 0 when the number of features reached ~99.

This is a demonstration of overfitting. With too many features, the model becomes increasingly accurate in describing the trend in the training data, but at the same time takes into account more noise from the training data that doesn’t generate to the rest of the data. As a result, validation scores decrease.

LASSO regularization

To fix overfitting, I experiment with LASSO regularization:

from sklearn.linear_model import Lasso

# generate data
n_train = 100
n_val = 100
noise = 0.2
train_scores = []
val_scores = []

# increase p_features from 1 to n_train-1 and calculate training and validation scores for each
for p_features in np.arange(1, n_train + 10): 
    # create data
    X_train, y_train, X_val, y_val = LR_data(n_train, n_val, p_features, noise)
    L = Lasso(alpha = 0.001)
    L.fit(X_train, y_train)
    train_scores.append(L.score(X_train, y_train))
    val_scores.append(L.score(X_val, y_val))


# plot
plt.plot(np.arange(1, n_train + 10), train_scores, label = "Training scores")
plt.plot(np.arange(1, n_train + 10), val_scores, label = "Validation scores")

xlab = plt.xlabel("Number of features")
ylab = plt.ylabel("Score")
legend = plt.legend()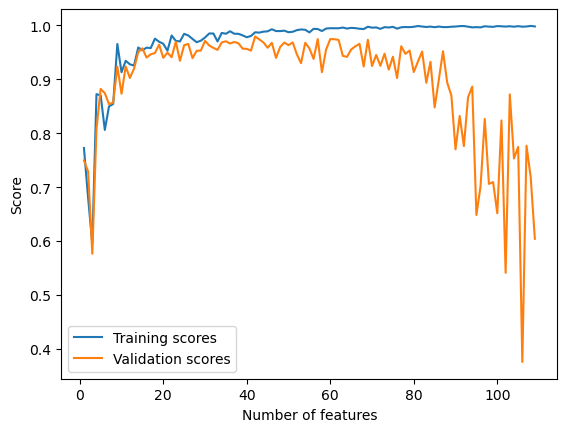

Using LASSO regularization, the validation scores still drops as the number of features increases, but there is no dramatical decrease as the number of features approaches, or even exceeds the number of data points. This is because LASSO is able to force entries of the weight vector to zero, which can help eliminate the effect of features that act as noise to the model.

Bikeshare data set

In this section, I train my linear regression model to a bikeshare data set.

# import data
import pandas as pd
from sklearn.model_selection import train_test_split
bikeshare = pd.read_csv("https://philchodrow.github.io/PIC16A/datasets/Bike-Sharing-Dataset/day.csv")

bikeshare.head()
instant dteday season yr mnth holiday weekday workingday weathersit temp atemp hum windspeed casual registered cnt
0 1 2011-01-01 1 0 1 0 6 0 2 0.344167 0.363625 0.805833 0.160446 331 654 985
1 2 2011-01-02 1 0 1 0 0 0 2 0.363478 0.353739 0.696087 0.248539 131 670 801
2 3 2011-01-03 1 0 1 0 1 1 1 0.196364 0.189405 0.437273 0.248309 120 1229 1349
3 4 2011-01-04 1 0 1 0 2 1 1 0.200000 0.212122 0.590435 0.160296 108 1454 1562
4 5 2011-01-05 1 0 1 0 3 1 1 0.226957 0.229270 0.436957 0.186900 82 1518 1600 
# plot the number of casual users over time
fig, ax = plt.subplots(1, figsize = (7, 3))
ax.plot(pd.to_datetime(bikeshare['dteday']), bikeshare['casual'])
ax.set(xlabel = "Day", ylabel = "# of casual users")
l = plt.tight_layout()

# transforming data
cols = ["casual", 
        "mnth", 
        "weathersit", 
        "workingday",
        "yr",
        "temp", 
        "hum", 
        "windspeed",
        "holiday"]

bikeshare = bikeshare[cols]

bikeshare = pd.get_dummies(bikeshare, columns = ['mnth'], drop_first = "if_binary")
bikeshare
casual weathersit workingday yr temp hum windspeed holiday mnth_2 mnth_3 mnth_4 mnth_5 mnth_6 mnth_7 mnth_8 mnth_9 mnth_10 mnth_11 mnth_12
0 331 2 0 0 0.344167 0.805833 0.160446 0 0 0 0 0 0 0 0 0 0 0 0
1 131 2 0 0 0.363478 0.696087 0.248539 0 0 0 0 0 0 0 0 0 0 0 0
2 120 1 1 0 0.196364 0.437273 0.248309 0 0 0 0 0 0 0 0 0 0 0 0
3 108 1 1 0 0.200000 0.590435 0.160296 0 0 0 0 0 0 0 0 0 0 0 0
4 82 1 1 0 0.226957 0.436957 0.186900 0 0 0 0 0 0 0 0 0 0 0 0
... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...
726 247 2 1 1 0.254167 0.652917 0.350133 0 0 0 0 0 0 0 0 0 0 0 1
727 644 2 1 1 0.253333 0.590000 0.155471 0 0 0 0 0 0 0 0 0 0 0 1
728 159 2 0 1 0.253333 0.752917 0.124383 0 0 0 0 0 0 0 0 0 0 0 1
729 364 1 0 1 0.255833 0.483333 0.350754 0 0 0 0 0 0 0 0 0 0 0 1
730 439 2 1 1 0.215833 0.577500 0.154846 0 0 0 0 0 0 0 0 0 0 0 1

731 rows × 19 columns

# train-test split
train, test = train_test_split(bikeshare, test_size = .2, shuffle = False)

X_train = train.drop(["casual"], axis = 1)
y_train = train["casual"]

X_test = test.drop(["casual"], axis = 1)
y_test = test["casual"]
# fit and score the model
LR = LinearRegression()
LR.fit(X_train, y_train)
LR.score(X_train, y_train)
0.7318355359284503

The model has a score of 0.73.

# compute predictions and visualize in comparison to actual test data
y_hat = LR.predict(X_test)

plt.plot(np.arange(len(y_hat)), y_hat, label = "Predictions")
plt.plot(np.arange(len(y_hat)), y_test, label = "Test data")
         
xlab = plt.xlabel("Day")
ylab = plt.ylabel("Number of casual users")
legend = plt.legend()

It seems that the model does a good job in predicting the general trend in the data – the overall decreasing number of users and the timing of peaks. However, it tends to underestimate the minimum and maximum values.

Finally, I will look into the weight vector and see what it reveals about people’s preference of when to use bikeshare.

# compare weight vector to list of features
feature_weights = pd.DataFrame(LR.w[:-1], X_train.columns)
feature_weights
0
weathersit -108.371136
workingday -791.690549
yr 280.586927
temp 1498.715113
hum -490.100340
windspeed -1242.800381
holiday -235.879349
mnth_2 -3.354397
mnth_3 369.271956
mnth_4 518.408753
mnth_5 537.301886
mnth_6 360.807998
mnth_7 228.881481
mnth_8 241.316412
mnth_9 371.503854
mnth_10 437.600848
mnth_11 252.433004
mnth_12 90.821460

We can observe a couple of interesting trends from the magnitude and direction of the weights: 1. People use bikeshare more when the weather is nicer – especially when it is warmer and there is less wind. It is also interesting, though, that the weathersit variable is slightly negatively correlated with the number of users. I wonder what exactly this variable is measuring. 2. People use bikeshare the most in April and May. This makes sense because weather is the best during this time of the year, while summer is too hot and winter is too cold. 3. People use bikeshare more on weekends but less on holidays.